Este artículo habla sobre la definición tradicional del diferencial, para otros usos dentro de la matemática vea diferencial (cálculo, desambiguación), para usos más generales vea diferencial (desambiguación)
En el campo de la matemática llamado cálculo, el diferencial representa la parte principal del cambio en la linealización de una función y = ƒ(x) con respecto a cambios en la variable independiente. El diferencial queda definido por la expresión
como si la derivada dy/dx representara el cociente entre la cantidad dy y la cantidad dx. Se puede también expresar como
El significado preciso de estas expresiones depende del contexto en las cuales se las utilice y el nivel de rigor matemático requerido. Según consideraciones matematicas rigurosas modernas, las cantidades dy y dx son simplemente variables reales y son manipuladas como tales. El dominio de estas variables puede tomar una significación geométrica particular si el diferencial es considerado como una forma diferencial, o significancia analítica si el diferencial es considerado como una aproximación lineal del incremento de la función. En aplicaciones físicas, a menudo se requiere que las variables dx y dy sean sumamente pequeñas (infinitesimales).
Definición
El diferencial está definido en los tratamientos modernos del cálculo diferencial de la siguiente manera. El diferencial de una función ƒ(x) de una única variable real x es la función df de dos variables reales e independientes x y Δx dada por:
Uno, o los dos, argumentos pueden ser suprimidos: ej., se puede ver df(x) o simplemente df. Si y = ƒ(x), el diferencial también puede ser escrito dy. Dado que dx(x, Δx) = Δx es convencional escribir dx = Δx, de manera que la igualdad
se mantiene.
1.2 Interpretación Geométrica:
El diferencial se puede tomar en el sentido geométrico como la elevación de la tangente desde el punto en que se toma el diferencial.
Recuérdese que la derivada de la función en el punto es la pendiente de la recta tangente a la función en el punto, como sabemos que la tangente de un ángulo es igual al cociente entre el cateto opuesto (incremento de y) y el cateto contiguo (incremento de x) de un hipotético triángulo rectángulo, sólo hay que despejar el incremento de y que equivale a nuestro diferencial.
Vista geométricamente, la elevación se produce verticalmente a partir del punto en que se toma el diferencial. El incremento  que se tome representará el alejamiento horizontal que haga desde el punto en cuestión.
que se tome representará el alejamiento horizontal que haga desde el punto en cuestión.
 que se tome representará el alejamiento horizontal que haga desde el punto en cuestión.
que se tome representará el alejamiento horizontal que haga desde el punto en cuestión.Así la elevación de la tangente que se obtenga como resultado dependerá del punto en cuestión y del alejamiento horizontal que se tomen, que en la formulas matemáticas están definidos respectivamente por  y
y  .
.
 y
y  .
.


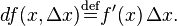
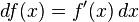

No hay comentarios:
Publicar un comentario