Las Matemáticas en la Administración: UNIDAD III: APLICACIONES DE LA DERIVADA

1. Valores máximos y mínimos de una Función y Extremos de una función.

1.1 Valores máximos y mínimos de una Función

Máximos
Si f y f' son derivables en a, a es un máximo relativo o local si se cumple:
1. f'(a) = 0
2. f''(a) < 0

Mínimos
Si f y f' son derivables en a, a es un mínimo relativo o local si se cumple:
1. f'(a) = 0
2. f''(a) > 0

Cálculo de los máximos y mínimos relativos
f(x) = x³ − 3x + 2
1. Hallamos la derivada primera y calculamos sus raíces.
f'(x) = 3x² − 3 = 0
x = −1 x = 1.

2. Realizamos la 2ª derivada, y calculamos el signo que toman en ella los ceros de derivada primera y si:
f''(x) > 0 Tenemos un mínimo.
f''(x) < 0 Tenemos un máximo.
f''(x) = 6x
f''(−1) = −6 Máximo
f'' (1) = 6 Mínimo

3. Calculamos la imagen (en la función) de los extremos relativos.
f(−1) = (−1)³ − 3(−1) + 2 = 4
f(1) = (1)³ − 3(1) + 2 = 0
Máximo(−1, 4) Mínimo(1, 0)

Ejercicios

1.2 Extremos de una función:

En matemáticas, los máximos y mínimos de una función, conocidos colectivamente comoextremos de una función, son los valores más grandes (máximos) o más pequeños (mínimos), que toma una función en un punto situado ya sea dentro de una región en particular de la curva (extremo local) o en el dominio de la función en su totalidad (extremo global o absoluto). De manera más general, los máximos y mínimos de un conjunto (como se define en teoría de conjuntos) son los elementos mayor y menor en el conjunto, cuando existen. El localizar valores extremos es el objetivo básico de la optimización matemática.

Extremos relativos o locales

Sea $f(x): A\sub\mathbb{R} \longrightarrow \mathbb {R}$ , sea $x_0 \in A$ y sea $P\,(x_0, f(x_0))$ un punto perteneciente a la función.

Se dice que

p

es un máximo local de

f

si existe un entorno reducido de centro

x 0

, en símbolos

E'(x 0)

, donde para todo elemento

x

E'(x 0)

se cumple $f(x) \le f(x_0)$ . Para que esta propiedad posea sentido estricto debe cumplirse

f(x) < f(x 0)

Análogamente se dice que el punto

p

es un mínimo local de

f

si existe un entorno reducido de centro

x 0

, en símbolos

E'(x 0)

, donde para todo elemento

x

E'(x 0)

se cumple $f(x) \ge f(x_0)$ .

Extremos absolutos

Sea $f(x): A\sub\mathbb{R} \longmapsto \mathbb {R}$ , sea $x_0 \in A$ y sea $P\,(x_0, f(x_0))$ un punto perteneciente a la función.

Se dice que P es un máximo absoluto de f si, para todo x distinto de

x 0

pertenenciente al subconjunto A, su imagen es menor o igual que la de

x 0

. Esto es:

$P\,(x_0, f(x_0))$ máximo absoluto de $f \iff \forall x \ne x_0, x \in A, f(x_0) \ge f(x)$ .

Análogamente, P es un mínimo absoluto de f si, para todo x distinto de

x 0

pertenenciente al subconjunto A, su imagen es mayor o igual que la de

x 0

. Esto es:

$P\,(x_0, f(x_0))$ mínimo absoluto de $f \iff \forall x \ne x_0, x \in A, f(x_0) \le f(x)$ .

Cálculo de extremos locales

Dada una función suficientemente derivable $f(x): A\sub\mathbb{R} \longrightarrow \mathbb {R}$ , definida en un intervalo abierto de $\mathbb {R}$ , el procedimiento para hallar los extremos de esta función es muy sencillo:

Se halla la primera derivada de $f \rightarrow f'\,(x)$
Se halla la segunda derivada de $f \rightarrow f''\,(x)$
Se iguala la primera derivada a 0: $f\,'(x) = 0$
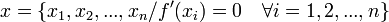Se despeja la variable independiente y se obtienen todos los valores posibles de la misma: $x = \big\{x_1, x_2,..., x_n / f'(x_i)= 0 \quad \forall i = 1,2,...,n \big\}$ .
Se halla la imagen de cada $x_i\,$ sustituyendo la variable independiente en la función.
Ahora, en la segunda derivada, se sustituye cada $x_i\,$ :
1. Si $f''\,(x_i) < 0$ , se tiene un máximo en el punto $M\, (x_i, f(x_i))$ .
2. Si $f''\,(x_i) > 0$ , se tiene un mínimo en el punto $m\, (x_i, f(x_i))$ .
3. Si $f''\,(x_i) = 0$ , debemos sustituir $x_i\,$ en las sucesivas derivadas hasta sea distinto de cero. Cuando se halle la derivada para la que $x_i\,$ no sea nulo, hay que ver qué derivada es:
  1. Si la derivada es par, se trata de un extremo local; un máximo si 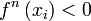$f^n\,(x_i) < 0$ y un mínimo si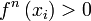 $f^n\,(x_i) > 0$
  2. Si la derivada no es par, se trata de un punto de inflexión, pero no de un extremo.

Ejemplo

Sea $f(x) = x^3 - 12x^2 + 45x -30 \,$ . Hallar sus extremos locales y sus puntos de inflexión.

Dada la función $f(x) = x^3 - 12x^2 + 45x - 30 \,$ , se tiene que:

$f'\,(x) = 3x^2 -24x + 45$

$f''\,(x) = 6x - 24$

$f'''\,(x) = 6$

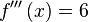
Extremos:

$f'\,(x) = 3x^2 - 24x + 45 = 0 \iff x \in \big\{3, 5\big\}$

$f''\,(3) = 6 \cdot 3 - 24 = -6 < 0 \Rightarrow$ existe un máximo en $M\,(3, f(3)) \rightarrow M\,(3, 24)$ .

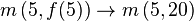$f''(5) = 6 \cdot 5 - 24 = 6 > 0 \Rightarrow$ existe un mínimo en $m\,(5, f(5)) \rightarrow m\,(5, 20)$ .

Puntos de inflexión

$f''(x) = 6x - 24 = 0 \iff x = 4$ .

$f'''(4) = 6 \ne 0 \Rightarrow$ existe un punto de inflexión en $P\,(4, f(4)) \rightarrow P\,(4, 22)$ .

Extremos condicionados

Un problema de extremos condicionados consiste en buscar un extremo de una función no sobre cualquier punto de su dominio sino sobre un subconjunto del dominio de la función que puede expresarse como variedad diferenciable. Más concretamente consiste en encontrar un máximo (o un mínimo) sujeto a la condición de que el punto donde se produce pertenezca a un cierto conjunto:

$\max_{x\in S} f(x), \qquad \left(\min_{x\in S} f(x)\right); \qquad \mbox{con}\ S:=\{x|g(x)=0\} \subset \R^n$

Este tipo de problemas aparece en numerosas aplicaciones prácticas tanto en ciencias físicas como incluso en economía. Para resolver este tipo de problemas se usa el método de los multiplicadores de Lagrange.

Las Matemáticas en la Administración

UNIDAD III: APLICACIONES DE LA DERIVADA

Extremos relativos o locales

Extremos absolutos

Cálculo de extremos locales

Ejemplo

Extremos condicionados

No hay comentarios:

Publicar un comentario