1.1 La derivada.
En matemáticas, la derivada de una función es una medida de la rapidez con la que cambia el valor de dicha función según cambie el valor de su variable independiente. La derivada de una función es un concepto local, es decir, se calcula como el límite de la rapidez de cambio media de la función en un cierto intervalo, cuando el intervalo considerado para la variable independiente se toma cada vez más pequeño. Por ello se habla del valor de la derivada de una cierta funciónen un punto dado.
Un ejemplo habitual aparece al estudiar el movimiento: si una función representa la posición de un objeto con respecto al tiempo, su derivada es la velocidad de dicho objeto. Un avión que realice un vuelo transatlántico de 4500 km en entre las 12:00 y las 18:00, viaja a una velocidad media de 750 km/h. Sin embargo, puede estar viajando a velocidades mayores o menores en distintos tramos de la ruta. En particular, si entre las 15:00 y las 15:30 recorre 400 km, su velocidad media en ese tramo es de 800 km/h. Para conocer su velocidad instantánea a las 15:20, por ejemplo, es necesario calcular la velocidad media en intervalos de tiempo cada vez menores alrededor de esta hora: entre las 15:15 y las 15:25, entre las 15:19 y las 15:21, etc.
El valor de la derivada de una función en un punto puede interpretase geométricamente, ya que se corresponde con pendiente de la recta tangente a la gráfica de la función en dicho punto. La recta tangente es a su vez la gráfica de la mejor aproximación lineal de la función alrededor de dicho punto. La noción de derivada puede generalizarse para el caso de funciones de más de una variable con la derivada parcial y el diferencial.
La derivada de una función f en un punto x se denota como f′(x). La función cuyo valor en cada punto x es esta derivada es la llamada función derivada de f, denotada por f′. El proceso de encontrar la derivada de una función se denomina diferenciación, y es una de las herramientas principales en el área de las matemáticas conocida como cálculo.
1.2 Definición:
En terminología clásica, la diferenciación manifiesta el coeficiente en que una cantidad  cambia a consecuencia de un cambio en otra cantidad
cambia a consecuencia de un cambio en otra cantidad  .
.
 cambia a consecuencia de un cambio en otra cantidad
cambia a consecuencia de un cambio en otra cantidad  .
.En matemáticas, coeficiente es un factor multiplicativo que pertenece a cierto objeto como una variable, un vector unitario, una función base, etc.
En física, coeficiente es una expresión numérica que mediante alguna fórmula determina las características o propiedades de un cuerpo.
En nuestro caso, observando la gráfica de la derecha, el coeficiente del que hablamos vendría representado en el punto  de la función por el resultado de la división representada por la relación
de la función por el resultado de la división representada por la relación  , que como puede comprobarse en la gráfica, es un valor que se mantiene constante a lo largo de la línea recta azul que representa la tangente en el punto
, que como puede comprobarse en la gráfica, es un valor que se mantiene constante a lo largo de la línea recta azul que representa la tangente en el punto  de la función. Esto es fácil de entender puesto que el tríangulo rectángulo formado en la gráfica con vértice en el punto
de la función. Esto es fácil de entender puesto que el tríangulo rectángulo formado en la gráfica con vértice en el punto  , por mucho que lo dibujemos más grande, al ser una figura proporcional el resultado de
, por mucho que lo dibujemos más grande, al ser una figura proporcional el resultado de  es siempre el mismo.
es siempre el mismo.
 de la función por el resultado de la división representada por la relación
de la función por el resultado de la división representada por la relación  , que como puede comprobarse en la gráfica, es un valor que se mantiene constante a lo largo de la línea recta azul que representa la tangente en el punto
, que como puede comprobarse en la gráfica, es un valor que se mantiene constante a lo largo de la línea recta azul que representa la tangente en el punto  de la función. Esto es fácil de entender puesto que el tríangulo rectángulo formado en la gráfica con vértice en el punto
de la función. Esto es fácil de entender puesto que el tríangulo rectángulo formado en la gráfica con vértice en el punto  , por mucho que lo dibujemos más grande, al ser una figura proporcional el resultado de
, por mucho que lo dibujemos más grande, al ser una figura proporcional el resultado de  es siempre el mismo.
es siempre el mismo.Esta noción constituye la aproximación más veloz a la derivada, puesto que el acercamiento a la pendiente de la recta tangente es tanto por la derecha como por la izquierda de manera simultánea.
En particular, se tiene que la derivada de la función en el punto  se define como sigue:
se define como sigue:
 se define como sigue:
se define como sigue: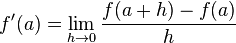 ,
,
Si este límite existe, de lo contrario, f' no está definida. Esta última expresión coincide con la velocidad instantánea del movimiento continuo uniforme acelerado en cinemática.
Aunque podrían calcularse todas las derivadas empleando la definición de derivada como un límite, existen reglas bien establecidas, conocidas como teoremas para el cálculo de derivadas, las cuales permiten calcular la derivada de muchas funciones de acuerdo a su forma sin tener que calcular forzosamente el límite. Tales reglas son consecuencia directa de la definición de derivada y de reglas previas, como puede apreciarse en todo buen texto de cálculo infinitesimal.
También puede definirse alternativamente la derivada de una función en cualquier punto de su dominio de la siguiente manera:
 ,
,
La cual representa un acercamiento de la pendiente de la secante a la pendiente de la tangente ya sea por la derecha o por la izquierda según el signo de  . El aspecto de este límite está relacionado más con la velocidad instantánea del movimiento uniformemente acelerado que con la pendiente de la recta tangente a una curva.
. El aspecto de este límite está relacionado más con la velocidad instantánea del movimiento uniformemente acelerado que con la pendiente de la recta tangente a una curva.
 . El aspecto de este límite está relacionado más con la velocidad instantánea del movimiento uniformemente acelerado que con la pendiente de la recta tangente a una curva.
. El aspecto de este límite está relacionado más con la velocidad instantánea del movimiento uniformemente acelerado que con la pendiente de la recta tangente a una curva.No obstante su aparente diferencia, el cálculo de la derivada por definición con cualquiera de los límites anteriormente expresados, proporciona siempre el mismo resultado.
El conocimiento de todas las expresiones anteriores y su significado representan el acercamiento epistémico más completo posible en torno a la definición de derivada, y con ello, al aspecto esencial del cálculo diferencial.
Existen diversas formas para nombrar a la derivada. Si f es una función, se escribe la derivada de la función  respecto al valor
respecto al valor  en varios modos:
en varios modos:
 respecto al valor
respecto al valor  en varios modos:
en varios modos: {Notación de Lagrange}
{Notación de Lagrange}
se lee «efe prima de equis»
 o
o  {Notaciones de Cauchy y Jacobi, respectivamente}
{Notaciones de Cauchy y Jacobi, respectivamente}
se lee « sub
sub  de
de  », y los símbolos D y d deben entenderse como operadores.
», y los símbolos D y d deben entenderse como operadores.
 sub
sub  de
de  », y los símbolos D y d deben entenderse como operadores.
», y los símbolos D y d deben entenderse como operadores. { Notación de Newton}
{ Notación de Newton}
se lee «punto  » o «
» o « punto». Actualmente está en desuso en Matemáticas puras, sin embargo se sigue usando en áreas de la física como la mecánica, donde otras notaciones de la derivada se pueden confundir con la notación de velocidad relativa. Se usa para definir la derivada temporal de una variable.
punto». Actualmente está en desuso en Matemáticas puras, sin embargo se sigue usando en áreas de la física como la mecánica, donde otras notaciones de la derivada se pueden confundir con la notación de velocidad relativa. Se usa para definir la derivada temporal de una variable.
 » o «
» o « punto». Actualmente está en desuso en Matemáticas puras, sin embargo se sigue usando en áreas de la física como la mecánica, donde otras notaciones de la derivada se pueden confundir con la notación de velocidad relativa. Se usa para definir la derivada temporal de una variable.
punto». Actualmente está en desuso en Matemáticas puras, sin embargo se sigue usando en áreas de la física como la mecánica, donde otras notaciones de la derivada se pueden confundir con la notación de velocidad relativa. Se usa para definir la derivada temporal de una variable. ,
,  ó
ó  {Notación de Leibniz}
{Notación de Leibniz}
se lee «derivada de  (
( ó
ó  de
de  ) con respecto a
) con respecto a  ». Esta notación tiene la ventaja de sugerir a la derivada de una función con respecto a otra como un cociente de diferenciales.
». Esta notación tiene la ventaja de sugerir a la derivada de una función con respecto a otra como un cociente de diferenciales.
 (
( ó
ó  de
de  ) con respecto a
) con respecto a  ». Esta notación tiene la ventaja de sugerir a la derivada de una función con respecto a otra como un cociente de diferenciales.
». Esta notación tiene la ventaja de sugerir a la derivada de una función con respecto a otra como un cociente de diferenciales.La notación más simple para diferenciación, en uso actual, es debida a Lagrange. Para identificar las derivadas de  en el punto a, se escribe:
en el punto a, se escribe:
 en el punto a, se escribe:
en el punto a, se escribe: para la primera derivada,
para la primera derivada, para la segunda derivada,
para la segunda derivada, para la tercera derivada,
para la tercera derivada, para la enésima derivada (n > 3). (También se pueden usar números romanos).
para la enésima derivada (n > 3). (También se pueden usar números romanos).
Para la función derivada de  en
en  , se escribe
, se escribe 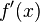 . De modo parecido, para la segunda derivada de
. De modo parecido, para la segunda derivada de  en
en  , se escribe
, se escribe  , y así sucesivamente.
, y así sucesivamente.
 en
en  , se escribe
, se escribe 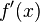 . De modo parecido, para la segunda derivada de
. De modo parecido, para la segunda derivada de  en
en  , se escribe
, se escribe  , y así sucesivamente.
, y así sucesivamente.La otra notación común para la diferenciación es debida a Leibniz. Para la función derivada de  , se escribe:
, se escribe:
 , se escribe:
, se escribe:Con esta notación, se puede escribir la derivada de f en el punto a de dos modos diferentes:
Si  , se puede escribir la derivada como
, se puede escribir la derivada como
 , se puede escribir la derivada como
, se puede escribir la derivada comoLas derivadas sucesivas se expresan como
 o
o 
para la enésima derivada de  o de y respectivamente. Históricamente, esto viene del hecho que, por ejemplo, la tercera derivada es
o de y respectivamente. Históricamente, esto viene del hecho que, por ejemplo, la tercera derivada es
 o de y respectivamente. Históricamente, esto viene del hecho que, por ejemplo, la tercera derivada es
o de y respectivamente. Históricamente, esto viene del hecho que, por ejemplo, la tercera derivada esla cual se puede escribir como
La notación de Leibniz es muy útil, por cuanto permite especificar la variable de diferenciación (en el denominador); lo cual es pertinente en caso de diferenciación parcial. También facilita recordar la regla de la cadena, porque los términos «d» parecen cancelarse simbólicamente:
En la formulación popular del cálculo mediante límites, los términos «d» no pueden cancelarse literalmente, porque por sí mismos son indefinidos; son definidos solamente cuando se usan juntos para expresar una derivada. En análisis no-estándar, no obstante, se puede ver como números infinitesimales que se cancelan.
La notación de Newton para la diferenciación respecto al tiempo, era poner un punto arriba del nombre de la función:
y así sucesivamente.
Esta notación de Newton se usa principalmente en mecánica, normalmente para derivadas de tiempo tales comos velocidad y aceleración, y en teoría de ecuaciones diferenciales ordinarias. Usualmente solo se usa para las primeras y segundas derivadas.
1.3 Interpretación Geométrica
Cuando h tiende a 0, el punto Q tiende a confundirse con el P. Entonces la recta secante tiende a ser la recta tangente a la función f(x) en P, y por tanto el ángulo α tiende a ser β.
La pendiente de la tangente a la curva en un punto es igual a la derivada de la función en ese punto.
Dada la parábola f(x) = x2, hallar los puntos en los que la recta tangente es paralela a la bisectriz del primer cuadrante.
La bisectriz del primer cuadrante tiene como ecuación y = x, por tanto su pendiente es m = 1.
Como las dos rectas son paralelas tendrán la misma pendiente, así que:
f'(a) = 1.
Porque la pendiente de la tangente a la curva es igual a la derivada en el punto x = a.
 1.4 Ecuaciones de la tangente a una curva
1.4 Ecuaciones de la tangente a una curva| |
| Ecuación de la recta tangente |
| Sea f una función continua en xo. La ecuación de la recta tangente a la curva en xo es: i) y = f '(xo) . x + b, si la función es derivable en xo.ii) x=xo, si la derivada, cuando x tiende a xo por la izquierda y por la derecha, es más infinito (o menos infinito). |
1. Derivamos la función f '(x)=3x2.
2. Evaluamos la derivada en 0,5, f '(0.5)=mt=0.75.
3. Calculamos la ordenada de xo=0.5 que es yo=f(xo)=1.13.
4. Sustituimos los valores dados en la ecuación de la recta tangente a la curva, es decir en yo=mt xo + b, para obtener b=0.75.
5. Escribimos la ecuación de la recta tangente: y = 0,75 x + 0,75
2. Cálculo de la ecuación de la recta tangente a y= sen x en xo=pi/2.
1. Derivamos la función y' = cos x.
2. Evaluamos la derivada en pi/2 para obtener mt= 0
3. Calculamos la ordenada de xo=pi/2, que es yo=1.
4. Calculamos la ordenada en el origen de la recta tangente, b=1.
5. Escribimos la ecuación de la recta tangente: y=1
3. Cálculo de la ecuación de la recta tangente a la siguiente curva en el punto de abscisa cero.
1. La derivada
2. Se observa que el dominio de la función es D=R, pero que la primera derivada no está definida en cero.
3. Analizando la derivada cuando x tiende a 0 por la izquierda y derecha se sabe que y' es más infinito en ambos casos, entonces la ecuación de la recta tangente es vertical y su ecuación: x=0
4. Cálculo de la ecuación de la recta tangente a la circunferencia x2 + y2 = 5 en xo= -2.
1. La derivada es y' = -(x/y) (Obtenerla derivando la función implícitamente).
2. La ordenada para xo= - 2 es yo= -1.
3. La derivada evaluada en (-2,1) es mt= - 2.
4. La ordenada en el origen de la recta tangente b= - 5.
5. La ecuación de la recta tangente: y = - 2x- 5
1.5 Ecuaciones de la Normal a una curva
Si se traza una perpendicular a la recta tangente se obtiene la recta normal. Los gráficos muestran la recta tangente y la normal a la curva en un punto dado.| Recta normal |
| La recta normal a la curva en el punto de abscisa xo es la recta perpendicular a la tangente a la curva en el mismo punto. |
| Pendiente y ecuación de la recta normal |
| i) Si la pendiente de la recta tangente es mt=f '(xo), la pendiente de la recta normal satisface la relación mt . mn = -1. y la ecuación de la recta normal: Yn = - 1/ f ´ (Xo) y = f(xo) |
5. Cálculo de la ecuación de la recta normal a y=x3+1 en xo=0,5.
1. Derivamos la función, y'=3x2.
2. Evaluamos la derivada en y'(0.5) = mt = 0.75.
3. Calculamos la pendiente de la recta normal mn= - 1.33.
4. Calculamos la ordenada de xo=0.5 que es yo=1.13.
5. Calculamos la ordenada en el origen de la recta normal, b=1.79.
6. Escribimos la ecuación de la recta normal:
yn = -1.33 x +1.79
1. Derivamos la función, y' = cos x.
2. Evaluamos la derivada en pi/2 para obtener mt= 0.
3. Calculamos la pendiente de la recta normal, mn= 1/0 = infinito. La recta normal forma un ángulo de 90º con el eje de las abscisas, es decir se trata de una recta vertical de ecuación
x = pi/2
7. Cálculo de la ecuación de la recta normal a la siguiente curva en el punto de abscisa cero.1. La derivada
2. La ecuación de la recta tangente es x=0 (recta vertical
3. La ecuación de la recta normal es y=f(xo), es decir
y=0
8. Cálculo de la ecuación de la recta normal a la circunferencia xo= -2 y con pendiente positiva.x2 + y2 = 5
1. La derivada es y' = -(x/y) (se obtiene derivando la función implícita).
2. La ordenada para xo= -2 es yo= -1.
3. La derivada evaluada en (-2,-1) es mt= - 2.
4. La pendiente de la recta normal, mt = 0.5.
5. La ordenada en el origen de la recta normal b=0.
6. La ecuación de la recta normal:
y= 0.5x

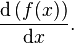







No hay comentarios:
Publicar un comentario