I. Limites y definición
1.1 Limites:
La noción de límite de una función en un numero (un punto de la recta real) se presentará mediante el siguiente ejemplo: Supongamos que se nos pide dibujar la gráfica de la función

Para todo punto x ≠ 1 podemos trazar la gráfica por los métodos conocidos por todos nosotros. Ahora, para tener idea del comportamiento de la gráfica de f cerca de x=1, usamos dos conjuntos de valores x, uno que se aproxime al 1 por la izquierda y otro por la derecha. La siguiente tabla muestra los correspondientes valores de f (x).
x se acerca al 1 por la izquierda  x se acerca al 1 por la derecha
x se acerca al 1 por la derecha
x | 0,9 | 0,99 | 0,999 | 1 | 1,001 | 1,01 | 1,1 |
f ( x ) | 2,71 | 2,9701 | 2,997001 | ¿? | 3,003001 | 3,0301 | 3,31 |
f (x) se acerca al 3  f (x) se acerca al 3
f (x) se acerca al 3

La figura 1 es la gráfica de la función y como podemos observar, en dicha gráfica hay un salto en el punto (1; 3), esto se debe a que la función f no está definida en el número 1. Es de notar que ésta gráfica es la de la función
y como podemos observar, en dicha gráfica hay un salto en el punto (1; 3), esto se debe a que la función f no está definida en el número 1. Es de notar que ésta gráfica es la de la función  menos el punto (1; 3). La función g se obtiene a partir de la función f, factorizando el numerador y simplificando. La discusión anterior conduce a la siguiente descripción informal: Si f(x) se aproxima arbitrariamente a un número L cuando x se aproxima a a por ambos lados, decimos que el límite f(x) cuando x tiende a a es L, y escribimos
menos el punto (1; 3). La función g se obtiene a partir de la función f, factorizando el numerador y simplificando. La discusión anterior conduce a la siguiente descripción informal: Si f(x) se aproxima arbitrariamente a un número L cuando x se aproxima a a por ambos lados, decimos que el límite f(x) cuando x tiende a a es L, y escribimos  .
.
1.2. Definición:
Sea f una función definida en todo número de algún intervalo abierto I que contiene a a excepto posiblemente en el número a mismo. El límite de f(x) cuando x se aproxima a a es L, lo cual se escribe como 
 , si para cualquier
, si para cualquier  , no importa que tan pequeña sea, existe una
, no importa que tan pequeña sea, existe una  tal que
tal que
si  entonces
entonces 
Esta indica que los valores de f(x) se aproximan al límite L conforme x se aproxima al número a, si el valor absoluto de la  puede hacerse tan pequeña como de desee tomando x suficientemente cerca de a pero no igual a a.
puede hacerse tan pequeña como de desee tomando x suficientemente cerca de a pero no igual a a.
En la definición no se menciona nada acerca del valor de f(x) cuando x = a; recordemos que la función no necesita estar definida en a para que  exista.
exista.
Ejemplos 1.
1) Utilicemos la definición para demostrar que 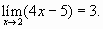
Como la función está definida en todo intervalo abierto que contiene a 2, entonces podemos utilizar la definición para hacer la demostración.
Se debe demostrar que para cualquier 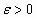 existe una
existe una 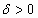 tal que
tal que
si 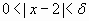 entonces
entonces 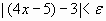 (A)
(A)
si 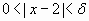 entonces
entonces 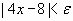
si 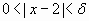 entonces
entonces 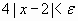
si 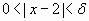 entonces
entonces 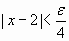
Entonces, si tomamos 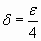 se cumple la proposición (A). Esto demuestra que
se cumple la proposición (A). Esto demuestra que 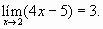
Tomando 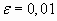 ,
, 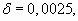 luego, para esos valores de
luego, para esos valores de 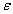 y
y 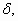 los números x que pertenecen al intervalo abierto
los números x que pertenecen al intervalo abierto 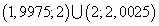 verifican la proposición(A). En efecto, tomando cualquier x en el intervalo anterior, por ejemplo x = 1,9976 se tiene:
verifican la proposición(A). En efecto, tomando cualquier x en el intervalo anterior, por ejemplo x = 1,9976 se tiene:
entonces
Esto verifica la proposición (A) para el valor específico tomado para x.
2) Demostrar usando la definición de límite que 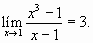
Como la función está definida en cualquier intervalo abierto que contenga al 1, excepto en el número 1, podemos aplicar la definición para realizar la demostración. En efecto,
si 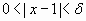 entonces
entonces 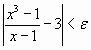 (B)
(B)
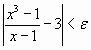 (B)
(B)si 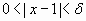 entonces
entonces 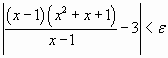
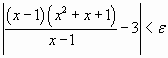
si 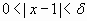 entonces
entonces 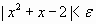
si 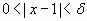 entonces
entonces 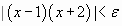
si 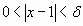 entonces
entonces 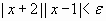
Ahora, cuando x se acerca a 1, x +2 se acerca a 3, luego, 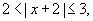 entonces,
entonces, 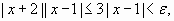 por lo tanto,
por lo tanto, 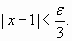 De la proposición (B) se obtiene que, si
De la proposición (B) se obtiene que, si 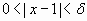 entonces
entonces 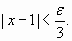 Si tomamos
Si tomamos 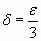 se cumple la proposición (B), lo que demuestra que
se cumple la proposición (B), lo que demuestra que 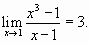

bienvenido al mundo de la Educacion Virtual
ResponderEliminarbuen inicio