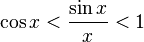Las Matemáticas en la Administración: 3. Limites al infinito, Limites infinitos, limites trigonométricos.

3.1 Limites al infinito:

Puedes darle clic al siguiente link para mayor información:
http://es.scribd.com/doc/62767321/limites-al-infinito

3.2 Limites infinitos:
Una función f(x) tiene por límite +∞ cuando x

a, si fijado un número real positivo K>0 se verifica que f(x)>k para todos los valores próximos a a.

Límite menos infinito

Una función f(x) tiene por límite -∞ cuando x

a, si fijado un número real

negativo K < 0 se verifica que f(x) < k para todos los valores próximos a.

3.3 Limites trigonométricos:

${\lim_{x \to \infty} x \; \sin \left (\frac {2\pi}{x} \right ) \cos \left (\frac {2\pi}{x} \right )} =\,2\pi$
${\lim_{x \to 0} {{\sin x} \over x}} = {\lim_{x \to 0} {{x \over \sin x}}} =\, 1 \,$
${\lim_{x \to 0} {\tan x \over x}} = {\lim_{x \to 0} {x \over \tan x}} =\, 1 \,$
${\lim_{x \to 0} {\sin x \over \tan x}}\, = {\lim_{x \to 0} {\tan x \over \sin x}} =\, 1$
${\lim_{x \to 0} \frac {1-\cos x}{x^2} } =\, 1/2 \,$

Demostraciones

Algunas demostraciones, por ejemplo, el segundo de estos límites trigonométricos, se utilizará la inecuación sin(x) < x < tan(x) en el intervalo (0,π/2), que relaciona x con las funciones seno y tangente. Luego dividimos por sin(x), obteniendo:

$1 < \frac{x}{\sin x} < \frac{1}{\cos x}$

Invirtiendo los términos de la inecuación y cambiando los signos de desigualdad:

$\cos x < \frac{\sin x}{x} < 1$

Calculando el límite cuando x tiende a 0:

$\lim_{x\to 0} \cos x < \lim_{x\to 0} \frac{\sin x}{x} < \lim_{x\to 0} 1$

Lo que es igual a:

$1 < \lim_{x\to 0} \frac{\sin x}{x} < 1$

Aplicando el teorema del sándwich o teorema de estricción, el límite necesariamente vale 1:

$\lim_{x\to 0}\frac{\sin x}{x}=1$

El tercero de los límites se demuestra utilizando las propiedades de los límites y el valor obtenido en el límite anterior. Es decir:

${\lim_{x \to 0} \left (\frac {\tan x}{x} \right )} = {\lim_{x \to 0} \left (\frac {\sin x}{x} \right )} \cdot \lim_{x \to 0} \frac{1}{\cos x}= 1 \cdot 1 = 1$